Distribusi Dalam Pemodelan dan Simulasi Sistem
Kegunaan Distribusi
Mengapa dibutuhkan penggunaan distribusi dalam pemodelan dan simulasi sistem ?
Karena simulasi pada umumnya memiliki data yang tidak tetap. Dan memiliki faktor ketidakpastian yang ada dalam masalah simulasi tidaklah mudah untuk menyelesaikan modelnya. Simulasi sangat cocok untuk mengamati sistem yang tidak pasti. Dengan adanya distribusi dalam pemodelan dan simulasi, dapat memperkirakan terjadinya peluang yang dihubungkan denga kemungkinan yang akan terjadi dalam kejadian pada keadaan tertentu. Dalam proses kemungkinan yang akan terjadi, dari kemungkinan tersebut akan membentuk distribusi. Dari distribusi yang didapat, distribusi tersebut menjelaskan melalu fungsi distribusi yang ada pada sebuah sistem.
Jenis-Jenis Distribusi
Diskret
- Geometric
- Binomial
- Poisson
- Uniform
- Bernoulli
Distribusi Binomial
Distribusi Binomial merupakan distribusi peluang yang dihasilkan dari proses Bernoulli yang memiliki empat karakteristik utama, yaitu:
1) Percobaan dilakukan pengulangan sebanyak n kali.
2) Tiap percobaan memiliki dua hasil saja yakni: sukses atau gagal.
3) Peluang sukses (p) pada setiap percobaan adalah konstan.
4) Pengulangan percobaan harus bebas (independent) satu sama lain, artinya hasil eksperimen yang satu tidak mempengaruhi hasil eksperimen yang lainnya.
Sebuah percobaan Bernoulli dengan peluang sukses p dan peluang gagal q = 1-p, maka distribusi peluang peubah acak binomial X (jumlah kejadian sukses dalam n kali percobaan) dapat dituliskan:
Peluang terambilnya kartu As di setiap pengambilan satu kotak kartu merupakan salah satu contoh percobaan Bernoulli.
Distribusi Hipergeometrik
Cara sederhana untuk membedakan distribusi Hipergeometrik dengan distribusi Binomial adalah dengan melihat proses penarikan sampelnya. Pada distribusi Binomial, antar percobaan bersifat bebas sedangkan pada distribusi Hipergeometrik peluang sukses percobaan saat ini bergantung pada hasil percobaan sebelumnya.
Percobaan Hipergeometrik memiliki sifat berikut:
1) Sampel acak ukuran n diambil tanpa pengembalian dari N benda
2) Sebanyak k benda dapat diberi nama sukses sedangkan sisanya, Nk, diberi nama gagal, sehingga distribusi peluang peubah acak Hipergeometrik X (banyaknya sukses dalam sampel acak ukuran n yang diambil dari N benda yang mengandung k bernama sukses dan N-k bernama gagal ialah :
Kontinu
- Exponential
- Gauss (normal)
- Gamma
- Weibull
- Negative Binomial
Distribusi Gauss
Distribusi Normal disebut juga Gausian distribution adalah salah satu fungsi distribusi peluang berbentuk lonceng seperti gambar berikut.
Berdasarkan gambar di atas, distribusi Normal akan memiliki beberapa ciri diantaranya:
1) Kurvanya berbentuk garis lengkung yang halus dan berbentuk seperti genta.
2) Simetris terhadap rataan (mean).
3) Kedua ekor/ ujungnya semakin mendekati sumbu absisnya tetapi tidak pernah mamotong.
4) Jarak titik belok kurva tersebut dengan sumbu simetrisnya sama dengan σ
5) Luas daerah di bawah lengkungan kurva tersebut dari – ~ sampai + ~ sama dengan 1 atau 100 %.
Distribusi Normal memiliki dua parameter yaitu rataan (µ) dan simpangan baku (σ). Jika X merupakan peubah acak, maka fungsi padat X dengan distribusi normal dinyatakan dengan
Distribusi Eksponensial
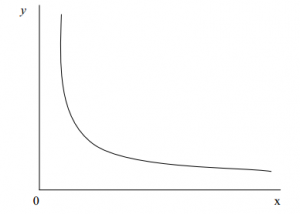
Distribusi Eksponensial memiliki pertalian erat dengan distribusi Poisson. Jika pada Poisson, peubah acak poisson X menggambarkan jumlah keluaran yang terjadi pada suatu selang waktu atau luas daerah tertentu, maka peubah acak Eksponensial X menggambarkan panjang rentang waktu antara suatu kejadian dengan kejadian lainnya. Gambar kurva distribusinya di gambarkan di bawah ini:
Dalam hal ini peubah acak X pada distribusi Poisson berkisar antara 0 sampai tak terhingga (0 < x <¥) dan bersifat kontinyu. Peubah acak kontinyu X berdistribusi Eksponensial dengan parameter b, fungsi densitasnya diberikan oleh:
Contoh Distribusi Dengan Nilai Acak
Pada software MINITAB, prosedur pengujian distribusi data tersedia dalam menu utama Stat, dilanjutkan dengan sub menu Quality Tools, pilih Individual Distribution Identification. Teknik pengujian distibusi yang ada dalam software ini adalah uji Anderson Darling dengan hipotesis statistik :
H0 : Distribusi data sesuai dengan distribusi yang diuji
H1 : Distribusi data tidak sesuai dengan distribusi yang diuji
Pengujian distribusi data dengan tingkat kesalahan (α) sebesar 0,05 akan memberikan keputusan bahwa distribusi yang diuji cocok dengan distribusi data, apabila p-value yang terhitung bernilai lebih besar dari 0,05. Berikut ini adalah hasil uji dari beberapa data set yang mempunyai nilai acak
Contoh hasil analisa distribusi dari data B,C dan D
Hasil uji kecocokan model yang dilakukan dengan uji Anderson Darling (AD) pada ketiga data diatas, disitrbusi weibull atau 3-Parameter Weibull memiliki p-value >= 0,05 dan bernilai paling tinggi dibandingkan dengan distribusi lainnya. Sehingga hasil uji telah memberikan bukti yang cukup bahwa data tersebut mengikuti distribusi Weibull atau 3-Parameter Weibull.
Adapun hasil analisa distribusi dari keseluruhan data, yaitu sebagai berikut :
Data A : Normal
Data B : Weibull
Data C : Weibull
Data D : Normal
Data E : Normal
Data F : Weibull
Distribusi Normal biasanya digunakan untuk menaksir dan meramalkan peristiwa-peristiwa yang lebih luas. Sedangkan, Distribusi Weibull biasanya digunakan untuk menyelesaikan masalah-masalah yang menyangkut lama waktu (umur) suatu objek yang mampu bertahan hingga akhirnya objek tersebut tidak berfungsi sebagaimana mestinya (rusak atau mati).
Referensi
http://www.rumusstatistik.com/2013/07/distribusi-weibull.html
http://repository.usu.ac.id/bitstream/123456789/26702/4/Chapter%20I.pdf
http://industri.ums.ac.id/sites/default/files/materi/Praktikum%20statistik%20MODUL%20II.pdf




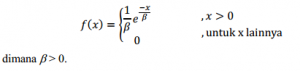




Terimakasih ilmunyaa